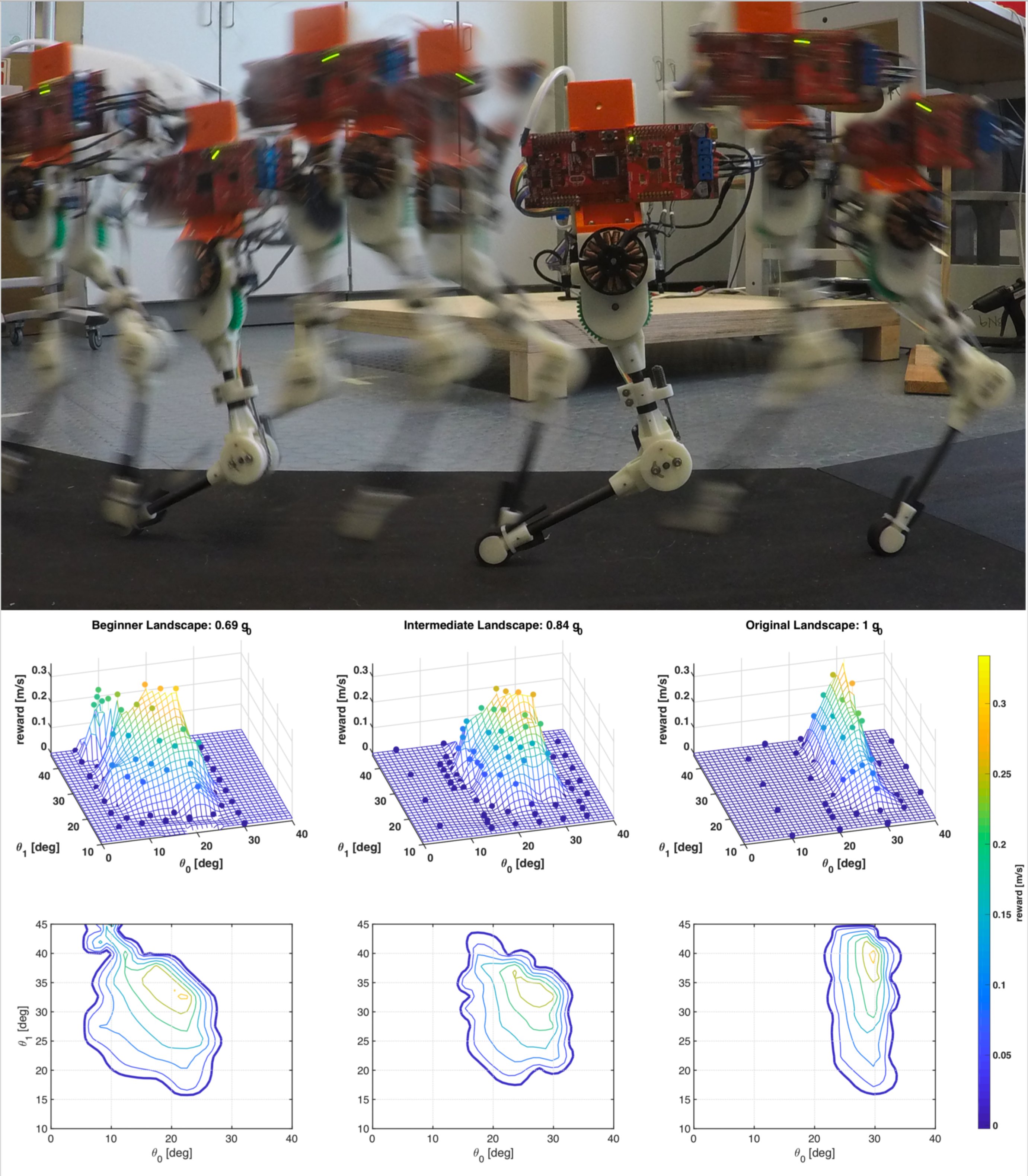
We can empirically map the true reward landscape of our monoped hopping robot, and observe the change of the landscape due to the modified effective weight of the system.
In reinforcement learning, tasks that are difficult to learn are often made more amenable by shaping the reward (cost) landscape. This is typically done by adjusting the reward signal $R$ in the Markov Decision Process, composed of $(S,A,P,R,\gamma)$, where $S$ is the state-space, $A$ is the action-space, $P$ is the probabiolity transition matrix (i.e. the system dynamics), $R$ is the reward signal and $\gamma$ is the discount factor.
We formalize and show the effectiveness of changing other parts of the MDP, in particular the dynamics $P$ and the initial state conditions $S_0$. The concept of training wheels, first formalized by [Randløv, 2001], uses instead a temporary adjustment of the system dynamics. As a practical example, we show that mechanically adjusting the weight of a hopping robot influences its reward landscape, resulting in learning that can occur more reliably and with less initial tuning [ ].
In a simple simulation, we show that state initialization can play an important role in state initialization. Indeed, we show that state initializations that are doomed to fail can not only be useful to learn effective policies, but they can result in much more reliable as well as quicker learning [ ].
